





Damien Michela, Antonis Argyrosa,b and Manolis Lourakisa
aInstitute of Computer Science,
Foundation for Research and Technology - Hellas
and
bDepartment of Computer Science,
University of Crete
Heraklion, Crete, Greece
Brief description: This work is concerned with the challenging problem of localizing an unordered set of central panoramic images, i.e. determining the relative positions and orientations of the viewpoints corresponding to the images at hand. The image set is assumed to be unordered, i.e. no a priori proximity ordering information is available as is the case for any image sequence. The localization problem arises naturally when dealing with distributed camera networks or vision-based mobile robot navigation (cf. the ``loop-closing'' and ``kidnapped robot'' problems). Our approach employs the Levenshtein distance to compare circular strings derived from image data confined to horizons. This limited cue is shown to suffice for registering the images in a common coordinate frame and partially reconstructing the environment. An early version of the approach has been published in OMNIVIS 2007.
A set of experiments was conducted in a laboratory room, sample panoramic images from which are shown on the left below (labeled A through F). The red line in each image corresponds to the location of the horizon. The locations and orientations of the viewpoints of these images are illustrated on the CAD floorplan of the room on the right.
 |
 |
 |
|
 |
|
 |
|
 |
|
 |
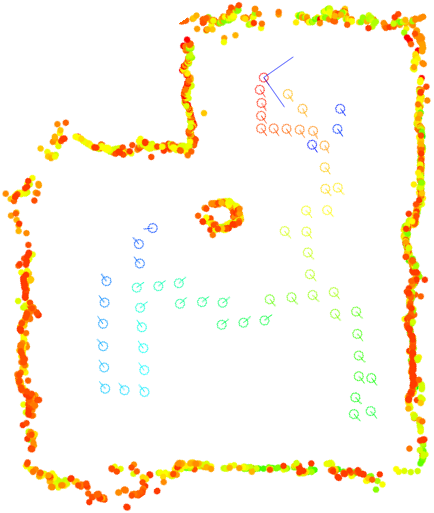
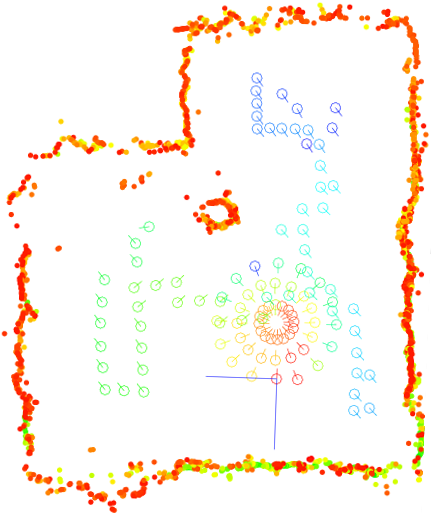
A video showing the progress of camera localization and structure estimation using an image set consisting of 61 images is here. It uses the Cinepak codec and its frames are 1024x768; it is recommended to view it at full size. A second video is also available, showing a similar result for the image set resulting from the combination of the previous 61 images with 48 more that were acquired on an trajectory consisting of three concentric circles. In both videos, the color of camera locations varies from red to blue in the order that the corresponding images are reconstructed. The color of reconstructed points varies from red to green according to the number of images from which they have been reconstructed: Red corresponds to points reconstructed from few images, green to those from many. The final reconstructions are also shown below.
 |
 |
For the previous experiment concerning the 109 images, the Levenshtein distance from all other horizons of the horizon line of a reference image on the inner circle has been computed. This distance was then plotted against the camera locations that were estimated through reconstruction. This video shows that 3D plot (the LD is on the Z axis assuming values between 0 to 1400) being rotated around various axes so that the relative differences among distances become visible. Evidently, the LD increases with the Euclidean distance of a location from that of the reference image.
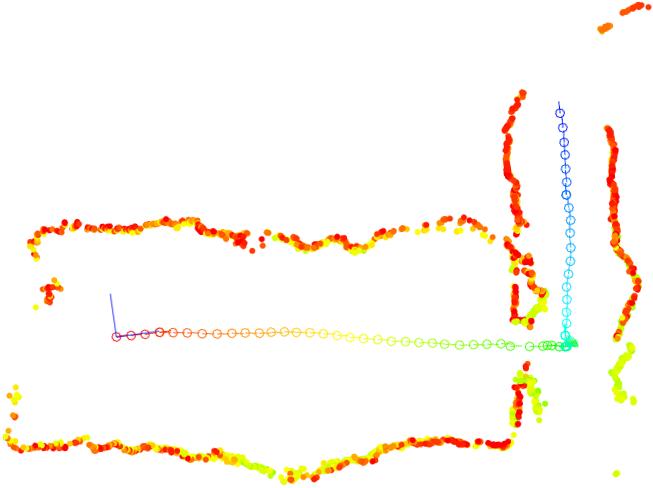
Yet another experiment was carried out with the aid of an image sequence that was captured by a panoramic camera mounted on top of a mobile robot that moved smoothly along an L-shaped trajectory. The robot started at one end of an oblong room, traversing it with constant velocity towards the opposite end on which the room's entrance is located. When the robot approached the entrance, it decelerated and exited the room into a corridor. Subsequently, the robot rotated in place for about 90o to align with the corridor and then moved along it. The recovered camera locations and environment map are shown below. This video shows the progress of camera localization combined with the image sequence.
 .
.
Page last changed on 29/2/2007.