 PROJECT BACKGROUND AND GOALS
PROJECT BACKGROUND AND GOALS PROJECT BACKGROUND AND GOALS
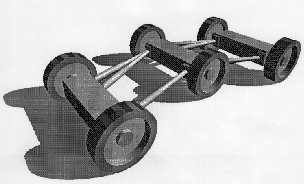
PROJECT BACKGROUND AND GOALSSystems with nonholonomic constraints are of particular interest to mobile robotics. Constraints of this type occur e.g. in wheeled robotic platforms, when their wheels roll without slipping, or in manipulators mounted on space platforms (space shuttle, satellites, space station), where the motion of the overall system conserves angular momentum. Nonholonomic motion planning problems aim at specifying paths for the system that respect those nonholonomic constraints and at designing control strategies that implement them. Our goal is to study the kinematics and motion control for a novel class of modular mobile manipulators which uses periodic variations of its shape in order to achieve snake--like locomotion.
|
|
 METHODOLOGY
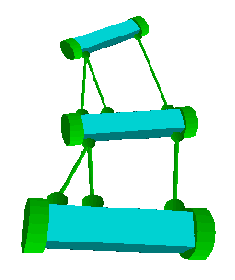
METHODOLOGY We consider Variable Geometry Truss (VGT) assemblies, which are structures consisting of longitudinal repetition of truss modules. In our case each module is implemented as a planar parallel manipulator consisting of two platforms connected by legs whose lengths can vary under the control of e.g. linear actuators, while each platform is equipped with a pair of wheels, so that it can move on the plane that supports the structure. The wheels of each pair are not actuated, their motion is independent of each other and we assume that they roll without slipping on the plane. This imposes a nonholonomic constraint on the motion of each platform, namely the requirement that its velocity is perpendicular to the axis connecting the wheels. When the legs of the individual modules are expanded or contracted the shape of the whole VGT assembly changes. Precisely because of the nonholonomic constraints, this shape change induces a global motion of the VGT assembly.
 PROJECT RESULTS
PROJECT RESULTSWe formulate the kinematics of a generic VGT assembly with L modules, which corresponds to a left--invariant system evolving on L copies of the Special Euclidean group G=SE(2), the group of rigid motions on the plane. The shape of each module corresponds to an element of G. The configuration of the VGT assembly can be described by the shape of its L modules and by the position and orientation of the assembly as a whole with respect to some fixed (world) coordinate system, which is given by another element of G. We consider the changes in the shape of each module as the controls of the VGT assembly. Those are expressed as elements of the Lie algebra of G and are called shape controls. The nonholonomic constraints allow us to make explicit the dependence of the global motion of the assembly on the shape controls. We specialize the previous discussion to the 2--module VGT. Unlike the generic L--module case, here we have exactly the number of nonholonomic constraints that we need in order to determine the position and orientation of the VGT assembly with respect to the world coordinate frame, based on a sequence of shape changes from a reference configuration. The geometric structure of the problem then becomes transparent. The nonholonomic constraints define a connection everywhere on a trivial principal fiber bundle, except for certain singular configurations. Away from the singular configurations, the connection helps us to compute the geometric phase of the VGT assembly, i.e. the global motion of the assembly induced by closed--loop shape--space trajectories under the nonholonomic constraints on the wheels. As a result, we consider the motion planning problem under a shape actuation scheme where one of the two modules is responsible for the propulsion of the assembly through periodic changes of its shape and the other module is responsible for steering. We demonstrate how to generate snake--like ``straight line motion'' and ``turning'' primitive behaviors and we show by simulations on Silicon Graphics IRIS workstations how to integrate them into more complex ones, such as avoidance of obstacles.
 FUTURE DIRECTIONS
FUTURE DIRECTIONSThe framework discussed here is being generalized to kinematic chains with nonholonomic constraints evolving on other Lie groups (H(3), SO(3), SL(2)). The collective name G-Snakes has been introduced for this class of systems. The corresponding optimal control problems (e.g. optimal shape variation that achieves a predetermined global motion) can be attacked using tools from Singular Riemannian geometry and our formulation is very appropriate for solving them. Finally, we can consider integration of this mechanical system with various obstacle avoidance and sensory information mediation schemes, in order to explore its motion in a constrained or dynamic environment.
 P.S. Krishnaprasad and D.P. Tsakiris,
"G-Snakes: Nonholonomic Kinematic Chains on Lie Groups",
33rd IEEE Conference on Decision and Control,
Lake Buena Vista, Florida, December 14-16, 1994.
P.S. Krishnaprasad and D.P. Tsakiris,
"G-Snakes: Nonholonomic Kinematic Chains on Lie Groups",
33rd IEEE Conference on Decision and Control,
Lake Buena Vista, Florida, December 14-16, 1994.
 P.S. Krishnaprasad and D.P. Tsakiris,
"2-Module Nonholonomic Variable Geometry Truss Assembly: Motion Control",
4th IFAC Symposium on Robot Control (SYROCO'94), Capri, Italy,
September 19-21, 1994.
P.S. Krishnaprasad and D.P. Tsakiris,
"2-Module Nonholonomic Variable Geometry Truss Assembly: Motion Control",
4th IFAC Symposium on Robot Control (SYROCO'94), Capri, Italy,
September 19-21, 1994.